3.1 A geocentric universe
3.1.1 Eudoxus and a geocentric universe
The ancient Greek mathematician Pythagoras suggested that the Earth is spherical in about 500 BCE, and this was accepted by most ancient Greek philosophers at the time.[1] Eudoxus of Cnidus, a student of ancient Greek philosopher Plato (discussed in Chapter 4), presented the first mathematical theory of the universe about a hundred years later.
Eudoxus’ model placed a spherical Earth at the centre of the universe. The Sun, planets, and stars were then placed in giant transparent spheres surrounding it.[2] A model of the universe that has the Earth at the centre is known as a geocentric model of the universe.
3.1.2 Aristotle and a finite, eternal, and geocentric universe
The ancient Greek philosopher Aristotle extended Eudoxus’ model of the universe in the 4th century BCE. Aristotle’s model of the universe was also geocentric, with the Sun, Moon, planets, and stars all orbiting the Earth inside of Eudoxus’ spheres. Aristotle believed the universe is finite in space but exists eternally in time.
Aristotle believed that space is fundamentally different from the Earth because he thought that objects in space are unchanging and move in perfect circles, which he considered to be the perfect shape. In contrast to this, the Earth is imperfect and constantly changing. Aristotle thought that comets must exist inside of the Earth’s sphere, as it was obvious that they didn’t move in perfect circles.[3,4]
Aristotle’s contemporary, ancient Greek astronomer Heraclides Ponticus, suggested that it would be simpler for the Earth to rotate than for the whole of the sky to orbit around it.[5] Ancient Greek astronomer Aristarchus of Samos went further and suggested that the Earth revolves around the Sun.[6] A model of the universe that has the Sun at the centre is known as a heliocentric model of the universe. These claims were generally dismissed, however, and Aristotle’s cosmology remained dominant in ancient Greece.
Figure 3.1 |
A geocentric universe depicted in 1660. |
Figure 3.2 |
A heliocentric universe depicted in 1660. |
3.1.3 Aristarchus and the distance to the Sun and Moon
Aristarchus attempted to calculate the relative distance between the Earth and the Sun in the 3rd century BCE. He did this by measuring the angle between the Moon and the Sun during a half moon and using trigonometry (discussed in Book II).
Figure 3.3 |
Aristarchus measured the relative distance between the Earth, Moon, and Sun by measuring the angle between the Moon and the Sun during a half moon. The ratio of the distances is given by the cosine of the angle. |
Aristarchus concluded that the Sun is about 20 times further away than the Moon and must be about 20 times larger. This is because the Moon and Sun appear to be the same size. This is most evident during solar eclipses when the Moon blocks out the Sun completely.[7] We now know that the Sun is almost 400 times further away than the Moon and it is about 400 hundred times larger.
3.1.4 Eratosthenes and the circumference of the Earth
Eratosthenes, who was the first person to measure the tilt of the Earth in about 240 BCE (discussed in Chapter 2), also measured the Earth's circumference.
Eratosthenes knew that the Sun would appear directly overhead in the Egyptian city of Swenet at noon on the day of the summer solstice (discussed in Chapter 2). This is the longest day of the year when the Sun is at its highest point in the sky.
Eratosthenes measured the angle of Sun in Alexandria at that time and found the difference between the two angles to be about 1/50 of a full circle. He realised that this meant the distance between Swenet and Alexandria must be 1/50 of the circumference of the Earth. He measured the distance between cities by timing how long it took to ride there by camel.
Eratosthenes concluded that the Earth has a circumference of about 252,000 stadia, which became the accepted value.[8] The Greek stadium was about 185 metres, and this leads to a circumference of 46,620 km, a slight overestimation.
If we assume that Eratosthenes used the Egyptian stadium of about 157.5 metres, however, then the circumference would have converted to 39,690 km, which is very close to the 40,030 km value accepted today.[9]
Figure 3.4 |
A diagram illustrating how Eratosthenes measured the circumference of the Earth. |
3.1.5 Ptolemy and epicycles
Ptolemy developed Aristotle’s geocentric theory of the universe in about 150 CE. Ptolemy knew that the planets don’t appear to orbit in perfect circles around the Earth.[10] Some planets, like Mars, even appear to move backwards before moving forwards again in large loops. Ptolemy suggested that planets like Mars move in circles as they orbit the Earth, where the circles are called epicycles.
Figure 3.5 |
The apparent motion of the Sun and planets from the Earth, depicted in 1777. |
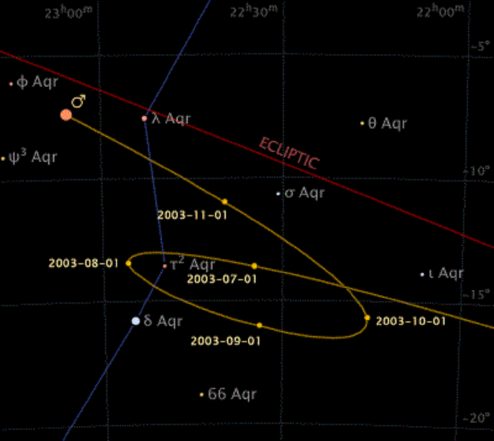
Figure 3.6 |
The apparent motion of the planet Mars in August and September 2003. |
Figure 3.7 |
Ptolemy’ universe was geocentric, with planets orbiting in epicycles. |
3.2 A heliocentric universe
3.2.1 Copernicus and a heliocentric universe
The Polish astronomer Nicolaus Copernicus reintroduced the idea of a heliocentric universe in On the Revolutions of the Celestial Spheres, first published in 1543. Like Ptolemy, Copernicus believed that the planets only travel in perfect circles, and so his heliocentric model needed a similar amount of epicycles to explain their observed motions.
The Catholic Church would not have accepted a realist heliocentric model, and so Copernicus presented his idea as a mathematical model. It provided an easier mathematical system for calculating where planets would be, but it was not to be taken literally.
Copernicus’ fears were not unfounded, almost 60 years later the Italian philosopher Giordano Bruno was burned at the stake for heresy after suggesting, among other things, that the Sun is just another star.[11]
3.2.2 Tycho and a changing universe
The Danish astronomer Tycho Brahe made some of the most accurate ever observations with the naked eye in the late 16th century. He disproved Aristotle’s concept of an unchanging universe when he saw a new star in the constellation of Cassiopeia in 1572. This was later identified as a supernova. Tycho also proved that Aristotle’s transparent spheres do not exist by showing that comets would have to travel through them.[12]
3.2.3 Kepler’s laws of planetary motion
Tycho’s student, German astronomer Johannes Kepler, first extended Aristotle’s theory of spheres by arguing that they are separated by five polyhedrons.
Polyhedrons are three-dimensional objects with sides that are all the same shape, like a cube, or a pyramid made of equilateral triangles. All of these shapes can be placed inside of a sphere so that the edges just touch the surface.[13,14]
Figure 3.8 |
Kepler’s first universe, from Mysterium Cosmographicum, 1596. |
Kepler also suggested that the planets might produce musical notes because they can be described with a frequency. This was based on Pythagoras’ idea that the universe can be represented in musical terms[15] (discussed in Book II).
Tycho later assigned Kepler the task of analysing his observations of Mars. Tycho’s data were accurate enough for Kepler to show, in 1609, that Mars’ orbit fits the shape of an ellipse, centred on a mass determined by the Sun and a second focal point.[16] This is Kepler’s first law.
Kepler’s second law, published at the same time, states that planets move faster when they are closer to the Sun.[16] This is due to the conservation of angular momentum (discussed in Chapter 4).
Kepler’s first law
“The orbit of every planet is an ellipse with the Sun at one of the two foci”.
Figure 3.9 |
Kepler’s first law. |
Kepler’s second law
“A line joining a planet and the Sun sweeps out equal areas during equal intervals of time”.
Figure 3.10 |
Kepler’s second law, where A is area and t is time. |
Kepler’s third law
“The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit”.
Figure 3.11 |
Kepler’s third law. |
By 1619, Kepler was able to determine the relationship between a planet’s average distance from the Sun and the time it takes to complete one orbit, its period.[15] While this did not allow him to calculate the actual speed or distance of each planet, he could work out the relative speeds and distances. Kepler showed that the Earth travels around the Sun at a faster speed than Mars, which explains the apparent loops in Mars’ orbit.
Figure 3.12 |
The apparent retrograde motion of Mars is caused by the Earth ‘overtaking’ Mars, as both planets orbit the Sun. |
3.2.4 Galileo and the telescope
Kepler’s contemporary, Galileo Galilei, added further proof to the heliocentric theory in 1610, when he made several observations that contradicted Aristotle.[17]
Galileo created one of the first microscopes and was one of the first people to use the telescope as an astronomical instrument.[18] This allowed him to became the first person to observe lots of phenomena, including the moons of Jupiter, the phases of Venus, sunspots, and the depth of the craters on the Moon, which he illustrated by showing the change in shadows across a day.
Galileo showed that not everything in space is perfect and unchanging, and that not everything orbits the Earth or the Sun.[17]
Galileo’s claims were accepted within a year, even though he didn't give enough information for others to replicate his results. Galileo was concerned that if others knew how to build a telescope like his, then they would beat him to all the potential new discoveries. He did distribute several telescopes, but these were sent to princes and cardinals, not astronomers or mathematicians.[19]
Despite this, Galileo’s observations were verified within a year by the Italian astronomer Antonio Santini. Santini sent a telescope to Kepler so he could verify them too.[19]
Christiaan Huygens showed that Saturn also has moons in 1655 when he discovered Titan. Huygens was also the first person to show that the bulges around Saturn are actually rings.[20]
Figure 3.13 |
Galileo’s sketches of the Moon from Sidereus Nuncius, 1610. |
Figure 3.14 |
Galileo’s sketches of sunspots from Istoria e Dimostrazioni Intorno Alle Macchie Solari e Loro Accidenti Rome, 1613. |
Figure 3.15 |
Galileo’s sketches of Jupiter’s moons from a draft letter written to Leonardo Donato, Doge of Venice, in 1609-1610. |
3.2.5 Galileo’s relativity
The heliocentric theory was easily dismissed at first because the Earth doesn’t appear to move. Galileo explained why we do not feel the movement of the Earth in 1632 with his theory of relativity.
If the Earth rotates, then its velocity (v) is equal to the distance it covers (d) divided by the time it takes (t).
| v = ΔxΔt = dΔt | (3.1) |
Here, Δ should be read as ‘change in’, t is time, and x is position, where a change in position is equal to a distance (d).
Velocity is a vector quality. This means that it contains two pieces of information: a value and a direction. The value, in this case, is the value of the speed. If the positive direction is defined as ‘right’ for example, then an object travelling 8 m/s to the right will have a velocity of 8 m/s, but if it is travelling to the left then it will have a velocity of -8 m/s.
In the case of the Earth’s rotation at the equator, the distance is the circumference of the Earth at the equator, which is about 40,030 km, and the time is equal to one day.
| v due to the Earth’s rotation | = | dΔt | (3.2) |
| = | 40,030,00060×60×24 | ||
| = | 463 m/s (1670 km/h) |
The velocity of the Earth around the Sun is,
| v due to the Earth’s orbit | = | dΔt | (3.3) |
| = | 942,478,000,00060×60×24×365.25 | ||
| = | 29,865 m/s (107,515 km/h) |
Here, 942,478,000,000 is the circumference (C) of the Earth’s orbit around the Sun in metres, where
| C = 2πr | (3.4) |
and r is the radius of the orbit. In this case, it is equal to the distance between the Earth and the Sun.
Galileo showed that we don’t feel this because of the principle of relativity. This shows that in a closed room there's no way of knowing whether you are moving at a constant velocity or whether you are stationary. When you are on a ship, for example, you are at rest with respect to the floor even though you are moving with respect to the sea.
Galileo stated,
Shut yourself up with some friend in the main cabin below decks on some large ship, and have with there flies, butterflies, and other small flying animals. Have a large bowl of water with some fish in it; hang up a bottle that empties drop by drop into a wide vessel beneath it. With the ship standing still, observe carefully how the little animals fly with equal speed to all sides of the cabin. The fish swim indifferently in all directions; the drops fall into the vessel beneath; and, in throwing something to your friend, you need throw it no more strongly in one direction than another, the distances being equal; jumping with your feet together, you pass equal spaces in every direction. When you have observed these things carefully (though there is no doubt that when the ship is standing still everything must happen in this way), have the ship proceed with any speed you like, so long as the motion is uniform and not fluctuating this way and that. You will discover not the least change in all the effects named, nor could you tell from any of them whether the ship was moving or standing still.[21]
A person on a ship may consider themselves to be stationary, with the shore moving away from them, and a person on the shore may consider themselves to be stationary while the ship moves away. No experiment can determine which perspective is correct, and so both views are equally valid.
This means that there’s no such thing as absolute speed or velocity. Something can only have a velocity relative to something else, and if there were only one object in the universe, there would be no way to know whether it was moving at a constant velocity or whether it was stationary.
Galileo also showed that relative speeds and velocities are additive. This means that if you walk at velocity u' across the deck of a ship that is moving at velocity v, then someone standing on the shore will measure your velocity to be u = v + u'. These observations influenced Albert Einstein’s theory of special relativity, published in 1905 (discussed in Chapter 7).
Galileo’s relativity is only applicable to objects that are stationary or travelling at constant velocities. You can feel the effect of acceleration (a), and this means that acceleration is not relative; there are always experiments that can determine if an object is changing velocity and hence accelerating.
| a = ΔvΔt | (3.5) |
People that are moving at a constant velocity (which can be zero) are said to be in an inertial frame of reference, and people that are accelerating are said to be in a non-inertial reference frame.
When objects move in a circle, they change direction, and so can change velocity without changing their speed. This acceleration is known as centripetal acceleration (ac), and it is always directed towards the centre of the circle.
If something is moving in a circle, then the direction can be measured in degrees. One full circle is 360°, which is equal to 2π radians, and so something moving at 8 m/s in a full circle, for example, will change velocity (Δv) by 2π × 8 m/s.
| ac = ΔvΔt = 2πv(2πrv) = v2r | (3.6) |
Here, r is the radius of the circle and v is the velocity of the object in a perpendicular direction to the acceleration (as shown in Figure 3.16). This is the same as the velocity calculated by dividing the circumference of the circle by the time.
Figure 3.16 |
Centripetal acceleration is always perpendicular to the direction of motion. |
The centripetal acceleration due to Earth’s rotation is,
| ac from Earth’s rotation | = | v2r | (3.7) |
| = | 46326,371,000 | ||
| = | 0.034 ms-2 (437 km h-2) towards the centre of the Earth. |
The centripetal acceleration due to Earth’s orbit around the Sun is,
| ac from Earth’s orbit | = | v2r | (3.8) |
| = | 29,8652150,000,000,000 | ||
| = | 0.006 ms-2 (77 km h-2) towards the Sun. |
In contrast to this, the acceleration we feel due to gravity (discussed in Chapter 2) is
| g = 9.8 ms-2 = 127,000 km h-2 | (3.9) |
The effect that we experience due to centripetal acceleration is minimal compared to the effect we feel from gravity. This is why we don’t notice it. However, it’s possible to conduct experiments to prove that something is accelerating, and so there are experiments that can prove that the Earth is moving.
3.2.6 Bradley and a moving Earth
In 1725, the English astronomer James Bradley attempted to prove that the Earth moves using a phenomenon known as stellar parallax. Stellar parallax occurs because the stars appear to move as we view them from slightly different positions throughout the year. Those that are closer appear to move more than those that are very far away.
Figure 3.17 |
Stellar parallax occurs because we view stars from different locations throughout the year. |
Bradley knew that if he could measure the angle that the stars appeared to move, then he could determine how far away they are using trigonometry. Tycho had failed to observe this movement, and Bradley’s observations were not able to provide evidence of parallax either, but he did observe stellar aberration.[22]
Stellar aberration is caused by the constantly changing angle with which we view the stars as the Earth orbits the Sun. It does not depend on the Earth’s change in position, and so it cannot be used to determine the distance to the stars, but it does show that the Earth is accelerating in the way we would expect if it were orbiting the Sun.
3.2.7 The size of the universe
The size of the known universe doubled in 1781 when the British astronomer William Herschel discovered the planet Uranus.[23] The size of the universe increased by a factor of over 8000 in 1838, shortly after German astronomer Friedrich Bessel first measured stellar parallax.
Bessel determined that the star 61 Cygni is about 10.4 light-years away.[24] This was quickly followed by the German astronomer Friedrich Georg Wilhelm von Struve’s announcement that the star Vega is about 26 light-years away.[25] Both were correct to within one light-year (a light-year is the distance that light travels in one year, and is equal to about 9000 billion km).
The German astronomer Johann Galle became the first person to observe the planet Neptune in 1846, following calculations made by French mathematician Urbain Le Verrier. The British astronomer William Lassell discovered Neptune’s largest moon Triton two and a half weeks later.[26]
The shape of the universe was refined once again in the 20th century, with the discovery of galaxies beyond the Milky Way (discussed in Chapter 10) and the expansion of the universe (discussed in Chapter 9).