7.1 19th Century problems with physics
In 1905, Albert Einstein combined the idea that experiments performed at a constant speed will give the same results as experiments that are stationary, with the idea that the speed of light will remain constant from both perspectives.[1] The first assumption is a result of Galileo’s relativity (discussed in Chapter 3). The second assumption comes from the Michelson-Morley experiment (discussed in Book II).
In 1632, Galileo Galilei showed that no experiment can distinguish if you are moving at a constant speed or velocity or if you are stationary without involving an external source, like a window to look out of.[2] This means that there’s no such thing as absolute speed or velocity, and something can only be said to be moving at a constant velocity relative to something else. In the same way, something can only be said to be stationary relative to something else.
Galileo also showed that speeds and velocities are additive. This means that if someone runs at speed u' across the deck of a ship moving at speed v, then the speed measured by someone on the shore (u) would be,
| u = v + u' | (7.1) |
If a beam of light were to move across the ship at speed c, the person on the shore should measure the speed to be u = v + c. In the same way, a person on Earth should measure the speed of light to be u = v + c, where v is the velocity of the Earth when it is moving towards the Sun.
In 1887, Albert Michelson and Edward Morley[3] measured the speed of light from the Sun while the Earth was moving in two different directions and found no difference (although the velocity was different because you can tell when light is moving towards or away from you, this did not affect the light’s speed). This was completely unexpected and showed that speeds and velocities are not additive, as Galileo had thought.
Special relativity shows that,
| u = v + u'1 + (vu'/c2) | (7.2) |
The speed of light is 299,792,458 m/s = 1,079,252,849 km/h. This means that if you are travelling on a ship at 5 km/h and run at 10 km/h. A person on the shore would measure your velocity to be about 15 km/h.
| u | = | 5 + 101 + (5×10 / 1,079,252,8492) | (7.3) |
| = | 151 + (50 / 1,079,252,8492) | ||
| = | 151.00000000000000004 | ||
| = | 14.9999999999999994 km/h |
If you run at 10 km/h (2.8 m/s) on a spacecraft travelling at 90% of the speed of light (269,813,212.2 m/s), then someone on Earth would measure your velocity to be slightly more than 90% of the speed of light but less than 269,813,212.2 m/s + 2.8 m/s.
| u | = | 269,813,212.2 + 2.81 + (269,813,212.2×2.8 / 299,792,4582) | (7.4) |
| = | 269813212.7 m/s |
However, if you shone a light from a spacecraft travelling at 90% of the speed of light, then someone on the shore would still measure the light's velocity to be the speed of light.
| u | = | 269,813,212.2 + 299,792,4581 + (269,813,212.2 / 299,792,458) | (7.5) |
| = | 569,605,670.21.9 | ||
| = | 299,792,458 m/s |
If the spacecraft was travelling at the speed of light,
| u | = | c + c1 + (c2/c2) = 2c2 = c | (7.6) |
7.2 Special relativity
If two people who are moving in different directions both measure the speed of light to be the same, then either of the two properties that speed relies on - time or distance - must differ between observers. Einstein’s theory of special relativity shows that both of these parameters can vary according to perspective. Special relativity, like Galileo’s relativity, applies to objects in an inertial reference frame - this means that it applies to objects that are not accelerating.
7.2.1 The relativity of simultaneity
The first consequence of special relativity is known as the relativity of simultaneity. This shows that events that appear simultaneous in one reference frame, might not do so in another.
If, for example, we place a light source between two observers that emits a beam of light in each direction, then the observers will think that the beams were emitted simultaneously if they reach each observer at the same time.
If the observers are moving, however, then the beams will not reach both observers at the same time, and so they may conclude that they were not emitted simultaneously. Galileo’s relativity shows that both views are correct. This means that what we perceive as the present only corresponds to what is occurring simultaneously to us, in our reference frame.
Figure 7.1 |
Events that appear simultaneous if you are stationary relative to them, may not do so if you are moving. |
7.2.2 Time dilation
The second consequence of special relativity is time dilation. This states that for someone in an inertial reference frame, moving clocks appear to run slower. This means that the time between ticks is longer.
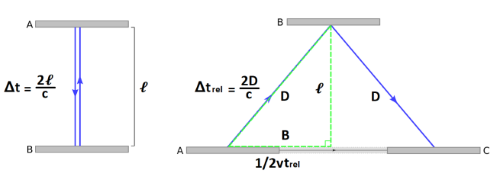
This can be illustrated by imagining that we bounce a beam of light from two mirrors and observe it from both perspectives, one where the mirrors are stationary with respect to the observer and one where the mirrors are moving (as shown in Figure 7.2).
Figure 7.2 |
Light must travel further if a clock appears to be moving than if it appears to be stationary, and so it takes a longer time. |
If the clock is stationary with respect to the observer, the light will travel vertically up and down, defined here as one tick. Assuming v = dΔt, where the distance is twice the length of the clock (ℓ).
| Δt = dv = 2ℓc | (7.7) |
The time we measure between events that are stationary with respect to someone in an inertial reference frame is known as ‘proper’ time, or rest time (t), and this is an invariant, which means that this value does not change, and could be calculated from any perspective. The time we measure between events that are moving with respect us is sometimes called relativistic time (trel).
If the clock is moving with respect to the observer, the mirrors will appear to be moving, and so the light will have to travel further between ticks. The distance is now equal to D.
| Δtrel = dv = 2Dc | (7.8) |
Using the Pythagorean theorem, D2 = ℓ2 + B2.
Figure 7.3 |
The Pythagorean theorem states that the square of the longest side of a right-angled triangle is equal to the sum of the squares of the other two sides. |
B is equal to half the distance the mirror moves between ticks, since d = vΔtrel, B = v Δtrel2.
This gives D2 = ℓ2 + (vΔtrel2), which is the same as D = √ℓ2 + ( vΔtrel2) , and Δtrel = 2Dc so that D = cΔtrel2.
This means √ℓ2 + ( vΔtrel2) = cΔtrel2, which can be rearranged to show,
| Δtrel = Δt√(1 - v2c2) | (7.9) |
This means,
| Δtrel = γΔt | (7.10) |
where,
| γ = 1√(1 - v2c2) | (7.11) |
γ is known as the Lorentz factor, as it’s derived from the work of the Dutch physicist Hendrik Lorentz. γ cannot be less than one, and so Δtrel is always larger than Δt. This is because it takes longer to travel a longer distance at the same velocity. If the time between ticks is longer, then the clock appears to be running slower; moving objects appear to be slowed in time.
The time between heartbeats is also slower, and so from the perspective of a stationary person, a moving person appears to be living their life at a slower rate. Conversely, from the perspective of the moving person, the stationary person seems to live like their life as if it is being fast-forwarded. If they travelled fast enough, then they would see the stationary person age before their eyes.
7.2.3 How much younger are astronauts when they return from space?
The Earth can be considered an approximately inertial reference frame because the effects of its acceleration (discussed in Chapter 3) are slight. This means that if a person leaves Earth and travels in a rocket at a constant velocity, then they will age more slowly than someone that stays on Earth. If they have a twin, then they will be younger than them when they return. This effect is greater the faster they travel.
If,
| Δt = time between ticks of a clock on Earth = 1 s, |
| v = velocity of moving person = 99% the speed of light = 296,794,533 m/s, and |
| c = 299,792,458 m/s. |
| Δtrel | = | γΔt = Δt√(1 - v2cv2) |
| = | 1√(1 - 296,794,5332299,792,4582) = 7 s |
This means that from the perspective of someone on Earth, it takes seven seconds for the astronaut’s clock to tick once; the astronaut’s actions appear to have slowed down.
If a person spends 6 months on the International Space Station, which travels at about 8 km/s, they will return about 0.0056 seconds younger than they would be if they had stayed on Earth.
| Δt = 6 months = 15,768,000 s, |
| v = velocity of moving person = 8 km/s = 8000 m/s, and |
| c = 299,792,458 m/s. |
| Δtrel | = | γΔt = Δt√(1 - v2c2) |
| = | 15,768,000√(1 - 80002299,792,4582) | |
| = | 15,768,000.0056 s | |
| Δtrel - Δt | = | 0.0056 s. |
Time dilation has a greater effect the higher the velocity and the longer the time spent at that velocity.
If a person spends 6 months travelling in a spacecraft at 99% of the speed of light, over 3 years would pass on Earth.
| Δt = 6 months = 15,768,000 s, |
| v = velocity of moving person = 296,794,533 m/s, and |
| c = 299,792,458 m/s. |
| Δtrel | = | 15,768,000√(1 - 296,794,5332299,792,4582) |
| = | 111,852,947 s = 3.54 years. |
If a person spends 6 months travelling in a rocket at 99.999% of the speed of light, over 100 years would pass on Earth, and if they were travelling at 99.99999999999% of the speed of light, over one million years would pass on Earth.
Figure 7.4 |
The time that people experience on Earth while an astronaut travels for 6 months at a range of velocities. |
The twin paradox asks why the astronaut can consider themselves to be moving and the Earth to be stationary, when Galileo’s relativity shows that there’s no such thing as absolute velocity. Why can’t the astronaut consider themselves to be stationary while the Earth moves away at tremendous speeds?
The answer is acceleration. Galileo’s relativity applies to inertial - that is non-accelerating - reference frames. The fact that the astronaut must have accelerated before getting to such a high speed means that they know they are the one that is moving.
7.2.4 Length contraction
The third consequence of special relativity is length contraction. Einstein showed that an object will appear to be shorter in its direction of motion if we measure it while it’s moving relative to us.
The length that we measure when we are stationary with respect to an object is known as the ‘proper’ length, or rest length. This is also an invariant. The length we measure if the object is moving with respect to us (ℓrel) is sometimes referred to as the relativistic length.
In the case of an astronaut travelling at 99% the speed of light (as discussed in Section 7.2.3), people on Earth measure 3.54 years to have passed before 6 months passes for the astronaut; Δt = 0.5 years and Δtrel = 3.54 years.
If the speed of light is the same from both perspectives, then they will each appear to have travelled different distances. From the perspective of someone on Earth, the astronaut travels for 0.5 years at 99% the speed of light. This means they will appear to cover a distance - or length - of about 0.5 light-years.
| ℓrel | = | vΔt | (7.12) |
| = | 296,794,533 × (0.5 × 60 × 60 × 24 × 365.25) | ||
| = | 4.68×1015 m | ||
| = | 0.5 light-years |
During this time, 3.54 years pass on Earth, and so the length would otherwise be about 3.5 light-years.
| ℓ | = | vΔtrel | (7.13) |
| = | 296,794,533 × (3.54 × 60 × 60 × 24 × 365.25) | ||
| = | 3.32×1016 m | ||
| = | 3.5 light-years |
This means that moving things appear to be shorter in their direction of motion.
| ℓrel | = | vΔt | (7.14) | |
| ℓ | = | vΔtrel | (7.15) | |
| Δtrel | = | Δtγ | (7.16) | |
| And so | ||||
| ℓrel | = | ℓγ | (7.17) |
ℓrel is always lower than ℓ, and so from the perspective of someone on Earth, the length of an astronaut’s rocket will appear shorter the faster it’s travelling.
If someone is travelling at 99% of the speed of light, their 7 km long spacecraft will seem 1 km wide to someone observing it on Earth.
| ℓrel | = | ℓ√(1 - v2c2) | (7.18) |
| = | 1√(1 - 296,794,5332299,792,4582) | ||
| = | 7 km |
Figure 7.5 |
The length of a spacecraft that people on Earth would measure to be 1 km wide at a range of velocities. |
7.2.5 Energy and momentum
Einstein’s theory of special relativity also alters our understanding of energy and momentum. Einstein imagined a mass at rest (m) that emits two photons – particles of light (discussed in Book II). One photon moves to the right and one to the left, as shown in Figure 7.6.
Figure 7.6 |
A stationary mass and moving mass before and after emitting two photons. |
The energy of something that is moving relative to an observer (erel) is related to the energy that would be measured if the object were at rest relative to the observer (e0) via,
| erel = γe0 | (7.19) |
And the relativistic momentum (prel) is,
| prel = γmv | (7.20) |
In Einstein’s example, the energy of the stationary mass is E0 before it emits the photons and E1 after. Due to the conservation of energy, E0 = E1 + e0, where e0 is the total energy of the photons that were emitted.
In the moving frame, the energy of the mass before it emits the photons is H0. This is the same as E0 except for the fact that it’s moving and so has some extra kinetic energy, H0 = E0 + KE0.
The energy of the mass after it emits the photons is H1, where H1 = E1 + KE1.
Due to the conservation of energy, H0 = H1 + γe0, where γe0 is the total energy of the photons that were emitted.
H1 is smaller than H0, and so the moving object loses energy when it emits the photons. This corresponds to a change in kinetic energy of,
| KE0 - KE1 | = | (H0 - E0) - (H1 - E1) | (7.21) |
| ΔKE | = | γe0 - e0 | (7.22) |
Einstein showed that unless v is very close to c, this becomes,
| ΔKE = 12 e0c2 v2 | (7.23) |
This means that when a moving object emits photons, it loses kinetic energy corresponding to a loss of mass equal to e0c2.
| e0 = mc2 | (7.24) |
The total energy (E) is equal to the rest energy plus the kinetic energy.
| E | = | e0 + KE | (7.25) |
| = | mc2 + (γe0 - e0) | (7.26) | |
| = | mc2 + (γmc2 - mc2) | (7.27) | |
| = | γmc2 | (7.28) |
Using p = γmv, where p = prel, this can be rearranged to show,
| E2 = p2c2 + m2c4 | (7.29) |
An object has no momentum if it is not moving, and so in this case,
| E = mc2 | (7.30) |
Some argue that special relativity implies that mass and energy are the same. The British physicist Arthur Eddington stated,
it seems very probable that mass and energy are two ways of measuring what is essentially the same thing, in the same sense that the parallax and distance of a star are two ways of expressing the same property of location.[4]
This is because the speed of light is equal to one if the distance is measured in light-years, and so E = m, although there is still much debate about the meaning of the energy-mass relationship.
An object that’s moving but has no mass, like a photon, will have an energy of E2 = p2c2 or,
| E = pc | (7.31) |
Classically, p = mv, and so something with zero mass should have zero momentum. Special relativity predicted that objects like photons do have a momentum, which can be calculated using an equation devised by the German physicist Max Planck in 1900 (discussed in Book II).
| E = hν | (7.32) |
Here ν is the light’s frequency, and h is a constant known as Planck’s constant. This gives pc = hν, and so p = hνc.
c = λ ν, where λ is the light’s wavelength, and so νc = 1λ giving,
| p = hλ | (7.33) |
The American physicist Arthur Compton proved this in 1922[5] (discussed in Book II).
Accelerating to the speed of light
An increase in kinetic energy is equal to the relativistic energy (erel) minus the rest energy (e0). ΔKE = γe0 - e0 = γmc2 - mc2, and so,
| KE = mc2(γ - 1) | and | γ = 1√(1 - v2c2) | (7.34) |
v2c2 = 1 when v = c, and so γ becomes 1√0 giving,
| KE = mc2(1√0 - 1) . | (7.35) |
This means that as v approaches c, the energy requirement approaches infinity.
7.2.6 Spacetime
In 1907 and 1908, the Polish-German mathematician Hermann Minkowski showed that special relativity is best described using the concept of a four-dimensional spacetime[6]. This unites the time dimension with the three spatial dimensions we observe.
Previous to this, the universe was described as an infinite three-dimensional space, with three spatial dimensions - x, y, and z - creating a cube-like, ‘flat’, space (as shown in Figure 7.7). This is known as Euclidean geometry, after ancient Greek mathematician Euclid. Objects could then be described by four coordinates: the three spatial coordinates and time (t). Newton described space and time as being absolute, which means that they are a background in which things take place. Here, the coordinate system is not affected by the objects it describes.
Minkowski showed that the coordinate system that describes an object’s location in spacetime does not have to be flat. He described spacetime as a 4-dimensional manifold. A manifold is a surface that looks flat from one perspective but may actually be curved. The surface of the Earth, for example, appears flat when we walk on it, but we know that the Earth is actually a sphere, and so only appears flat from a limited perspective. The locations of objects in spacetime are still described by four coordinates.
Figure 7.7 |
In Newtonian physics, space could be described using a Cartesian coordinate system in three dimensions. |
Figure 7.8 |
Minkowski showed that the coordinate systems that describe spacetime do not have to be flat. |
In special relativity, spacetime is thought to be flat and Cartesian coordinates are used, however in general relativity (discussed in Chapter 8), this is not the case, and there is no one unique coordinate system that must be used. In Minkowski’s spacetime, the ‘distance’ between two events can be described as a ‘spacelike’, ‘timelike’, or ‘ lightlike’ interval.
Spacelike intervals
If two events appear simultaneous to someone that’s not accelerating with respect to the events, then they are said to be separated by a spacelike interval.
Timelike intervals
If two events describe the same object in different locations, then they are said to be separated by a timelike interval. If all of the past, present, and future events that happen to a single object are placed on a plot of space against time (as shown in Figure 7.9), then the line connecting them all is referred to as a ‘worldline’, and two events on a worldline are always connected by timelike intervals.
Figure 7.9 |
The worldline of the Earth as it orbits the Sun. The Earth’s path through space is almost circular, but it’s constantly moving forward in time. |
Lightlike intervals
If a ray of light could travel between two events, then they are said to be separated by a lightlike interval. Plots of space against time produces cone shapes, known as light cones, for objects travelling at the speed of light (as shown in Figure 7.10). This is because in special relativity, unlike Newtonian physics, there’s a universal speed limit; things cannot happen instantaneously. An event in spacetime can only affect the areas it can physically reach, given that information cannot travel faster than the speed of light.
Light reaches further regions of space over time, and this means the future light cone gets wider as time goes on. The past light cone gets wider the further you look back in time because you see further back in time the further you look out into space. This is because light takes a long time to reach us, and so to see something as it was a long time ago, the light must originate from far away. We cannot be affected by anything that is too far away for its light to reach us.
Figure 7.10 |
The light from an event in spacetime can be mapped in 3-D with time as the vertical dimension. |
Special relativity was still not compatible with Newton’s law of universal gravitation because objects accelerate under gravity, and special relativity only tends to apply to objects that are moving at a constant velocity. The concept of mass and its effect on spacetime were better understood when Einstein reconciled his theory of special relativity with Newton’s law of universal gravitation. He finally achieved this in 1916, with his theory of general relativity.[7]
Why can’t we remember the future?
The obvious answer is that we can’t remember the future because it hasn’t happened yet, but this isn’t the whole story.[8] There are two ways to look at time:[9]
- The tensed theory of time states that time is something that flows, as the present moves away from the past and towards the future. This is the most natural way to think of time and, if this theory is correct, then we are right to conclude that we can’t remember the future because it hasn’t happened yet. The problem is, there’s no physical theory that requires time to flow, and on a microscopic level, all physical processes would still make sense if time were reversed.[10]
- The tenseless theory of time states that time is static, the past is just as real as the future and our experience of the present is an illusion. If there’s no such thing as the flow of time, then all times are equally real and the universe can be thought of as a complete and unchanging ‘block’ of four-dimensional spacetime. Given that the tenseless theory of time is correct, and that the future is as real as the past, then it makes sense to ask why we can’t we remember the future.
We may have evolved to experience the flow of time because it provides an evolutionary advantage.[9] The illusion of the flow of time may have evolved to mimic the thermodynamic arrow of time, which is defined by the law of entropy, also known as the second law of thermodynamics.[11] This states that a closed system will become increasingly disordered over time, assuming that its components move randomly.
If our perception of the flow of time is an illusion created by the brain, then we may be able to overcome this with technology. It may also be possible that other forms of life have evolved to experience the world without the concept of the present. Some propose that it’s not possible for a conscious being to remember the future because if they knew what they were going to do, then they could choose to act differently, therefore proving that their future memory was false and creating a paradox.[12]
Others worry that a tenseless view of time contradicts our notion of free will, even with the illusion of the flow of time.[13] This is because if our future is just as real as our past, then it must be ‘fixed’, whether we know it or not. This problem is not exclusive to the tenseless view of time. Many neurophysiologists have confirmed that human behaviour can be predicted. In 2008, Chun Siong Soon and colleagues showed that you can predict a person’s free choice up to 10 seconds before they are aware of what they will do.[14]
However, determinism is not necessarily incompatible with free will. This is because the two concepts are not mutually exclusive. We are considered to be acting freely when we act consistently with our character. In fact, people may question the freedom of our actions if we began to act drastically out of character. In 1954, the British philosopher Alfred Jules Ayer argued that free will should be contrasted with constraint, not determinism.[15]